前言
以前对于排序,只知道冒泡排序,了解一点快速排序,一直是我的弱点,今天是时候好好攻克一下了
参考:JS中可能用得到的全部的排序算法
时间复杂度
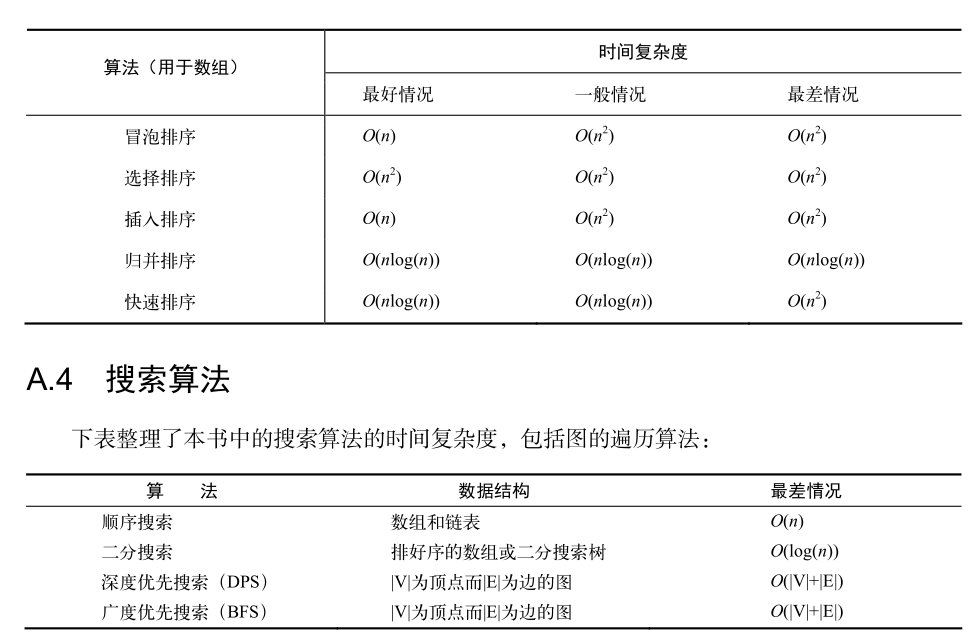
1、冒泡排序
冒泡排序需要两个嵌套的循环. 其中, 外层循环移动游标; 内层循环遍历游标及之后(或之前)的元素, 通过两两交换的方式, 每次只确保该内循环结束位置排序正确, 然后内层循环周期结束, 交由外层循环往后(或前)移动游标, 随即开始下一轮内层循环, 以此类推, 直至循环结束.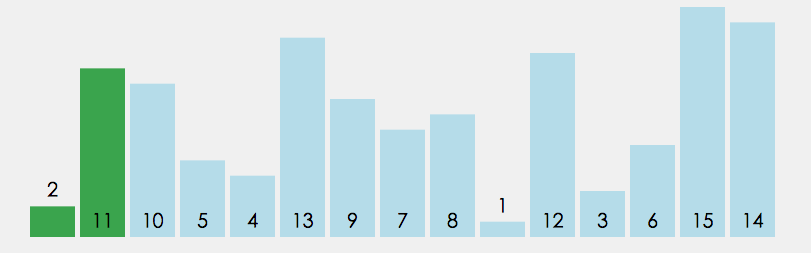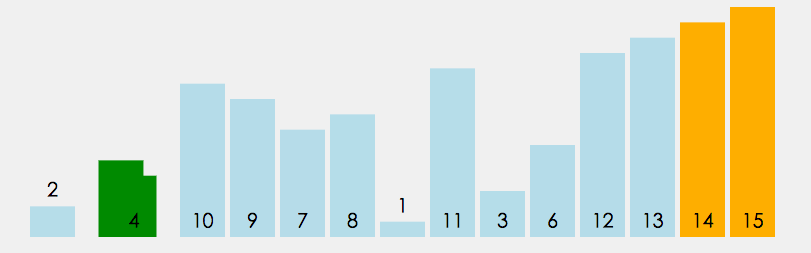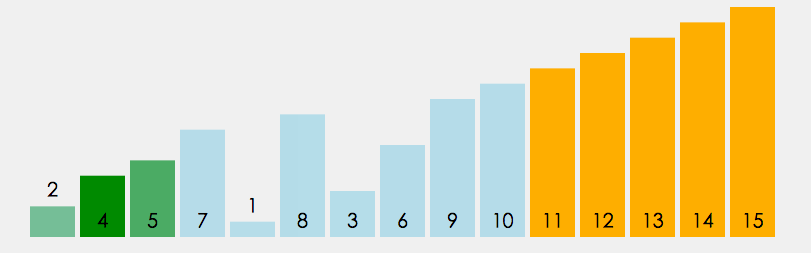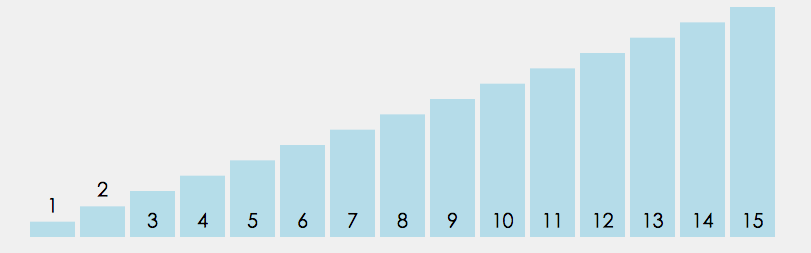
1 | // 交换下标a、b对应的数组数值,此方法抽离处理,后面直接使用,不做说明 |
1 | function sort(array) { |

2、双向冒泡排序
双向冒泡排序是冒泡排序的一个简易升级版, 又称鸡尾酒排序. 冒泡排序是从低到高(或者从高到低)单向排序, 双向冒泡排序顾名思义就是从两个方向分别排序(通常, 先从低到高, 然后从高到低). 因此它比冒泡排序性能稍好一些.
1 | function sort(array) { |
3、选择排序
从算法逻辑上看, 选择排序是一种简单且直观的排序算法. 它也是两层循环. 内层循环就像工人一样, 它是真正做事情的, 内层循环每执行一遍, 将选出本次待排序的元素中最小(或最大)的一个, 存放在数组的起始位置. 而 外层循环则像老板一样, 它告诉内层循环你需要不停的工作, 直到工作完成(也就是全部的元素排序完成).
Tips
: 选择排序每次交换的元素都有可能不是相邻的, 因此它有可能打破原来值为相同的元素之间的顺序. 比如数组[2,2,1,3], 正向排序时, 第一个数字2将与数字1交换, 那么两个数字2之间的顺序将和原来的顺序不一致,虽然它们的值相同, 但它们相对的顺序却发生了变化. 我们将这种现象称作不稳定性.
1 | /** 3、选择排序 **/ |
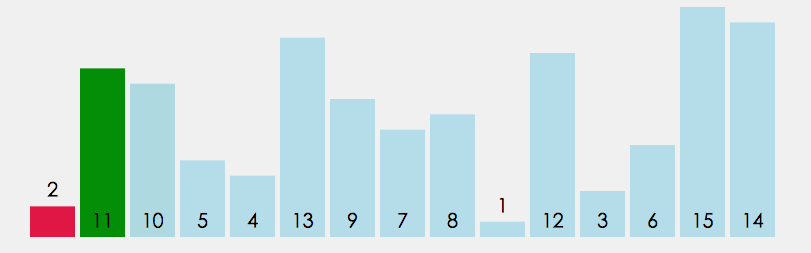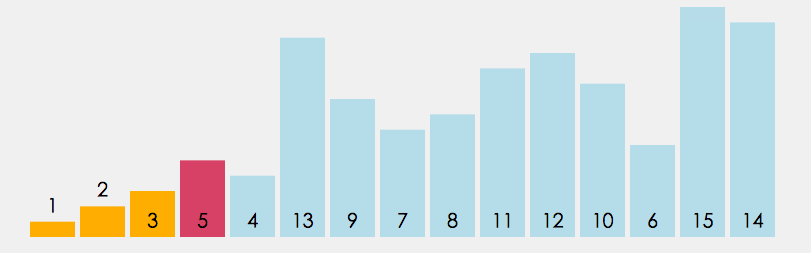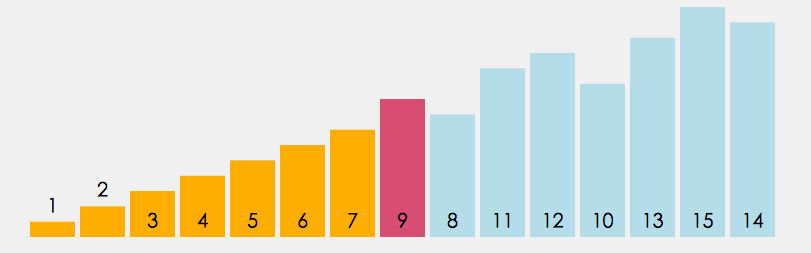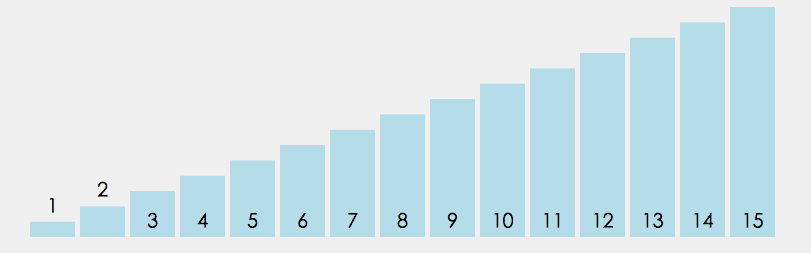

插入排序
插入排序的设计初衷是往有序的数组中快速插入一个新的元素. 它的算法思想是: 把要排序的数组分为了两个部分, 一部分是数组的全部元素(除去待插入的元素), 另一部分是待插入的元素; 先将第一部分排序完成, 然后再插入这个元素. 其中第一部分的排序也是通过再次拆分为两部分来进行的.
插入排序由于操作不尽相同, 可分为 直接插入排序 , 折半插入排序(又称二分插入排序), 链表插入排序 , 希尔排序 .
4、直接插入排序
它的基本思想是: 将待排序的元素按照大小顺序, 依次插入到一个已经排好序的数组之中, 直到所有的元素都插入进去.
由于直接插入排序每次只移动一个元素的位置, 并不会改变值相同的元素之间的排序, 因此它是一种稳定排序.
1 | /** 4、直接插入排序 **/ |
5、折半插入排序
折半插入排序是直接插入排序的升级版. 鉴于插入排序第一部分为已排好序的数组, 我们不必按顺序依次寻找插入点, 只需比较它们的中间值与待插入元素的大小即可.
说白一点就是从第二个数开始向前比较,前面的数(已经排好序)分成两半,找到中间的数,比较大小,然后在向中间循环,一直找到介于两者之间的,然后把之后的后移,将此值插入到后移留出来的位置。
和直接插入法相比,少了一半数据量的对比。
算法基本思想是:
- 取0 ~ i-1的中间点( m = (i-1)>>1 ), array[i] 与 array[m] 进行比较, 若array[i] < array[m] , 则说明待插入的元素array[i] 应该处于数组的 0 ~ m 索引之间; 反之, 则说明它应该处于数组的 m ~ i-1 索引之间.
- 重复步骤1, 每次缩小一半的查找范围, 直至找到插入的位置.
- 将数组中插入位置之后的元素全部后移一位.
- 在指定位置插入第 i 个元素.
1 | /** 5、折半插入排序 **/ |
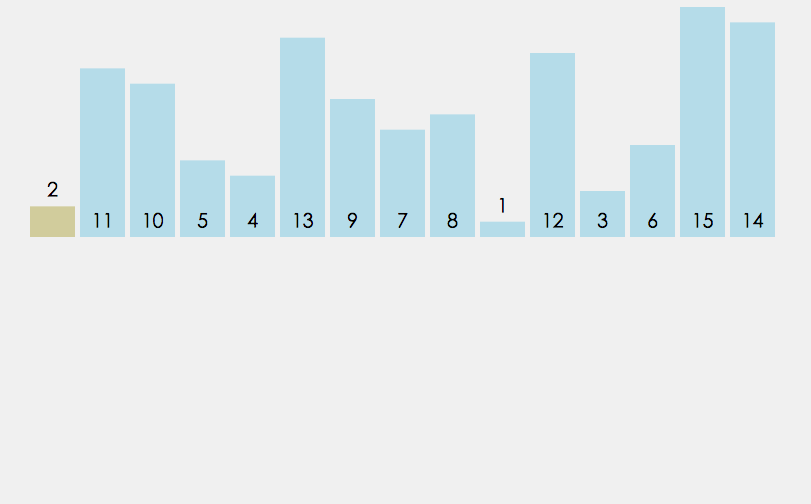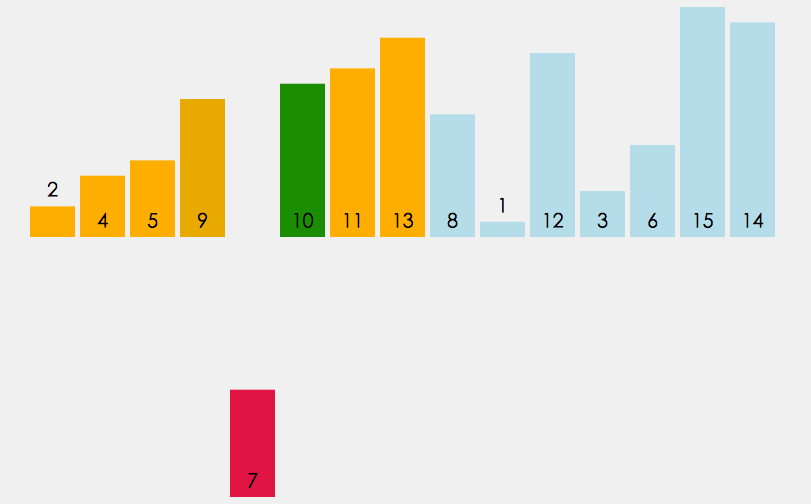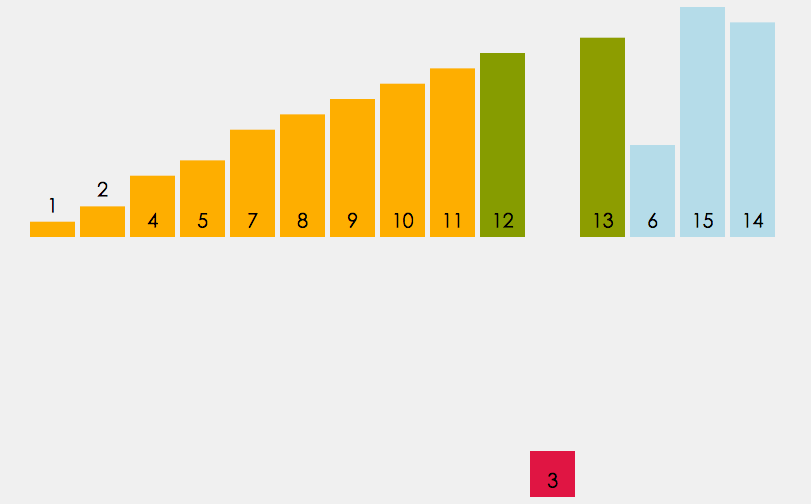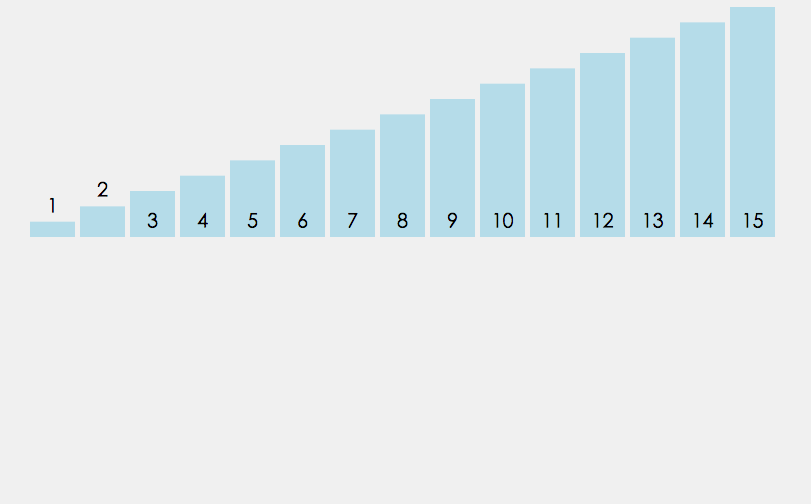
6、希尔排序
希尔排序也称缩小增量排序, 它是直接插入排序的另外一个升级版, 实质就是分组插入排序. 希尔排序以其设计者希尔(Donald Shell)的名字命名, 并于1959年公布.
算法的基本思想:
- 将数组拆分为若干个子分组, 每个分组由相距一定”增量”的元素组成. 比方说将[0,1,2,3,4,5,6,7,8,9,10]的数组拆分为”增量”为5的分组, 那么子分组分别为 [0,5], [1,6], [2,7], [3,8], [4,9] 和 [5,10].
- 然后对每个子分组应用直接插入排序.
- 逐步减小”增量”, 重复步骤1,2.
- 直至”增量”为1, 这是最后一个排序, 此时的排序, 也就是对全数组进行直接插入排序.
示意图: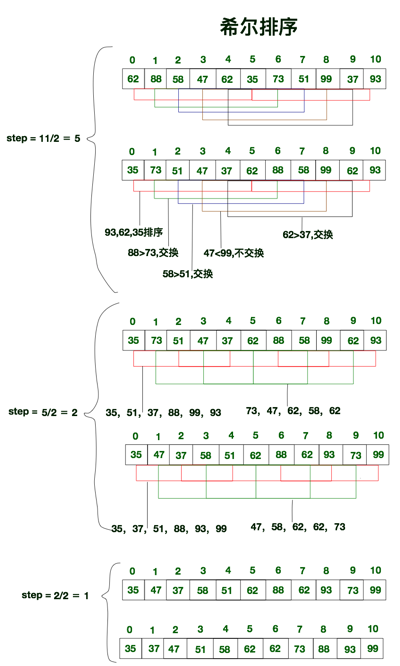
可见, 希尔排序实际上就是不断的进行直接插入排序, 分组是为了先将局部元素有序化. 因为直接插入排序在元素基本有序的状态下, 效率非常高. 而希尔排序呢, 通过先分组后排序的方式, 制造了直接插入排序高效运行的场景. 因此希尔排序效率更高.
1 | /** 6、希尔排序 **/ |
7、快速排序
这是一种使用非常广泛的排序,典型的代表就是Chrome的v8引擎为了高效排序, 在排序数据超过了10条时, 便会采用快速排序. 对于10条及以下的数据采用的便是插入排序
快速排序”的思想很简单,整个排序过程只需要三步:
(1)在数据集之中,选择一个元素作为”基准”(pivot)。
(2)所有小于”基准”的元素,都移到”基准”的左边;所有大于”基准”的元素,都移到”基准”的右边。
(3)对”基准”左边和右边的两个子集,不断重复第一步和第二步,直到所有子集只剩下一个元素为止。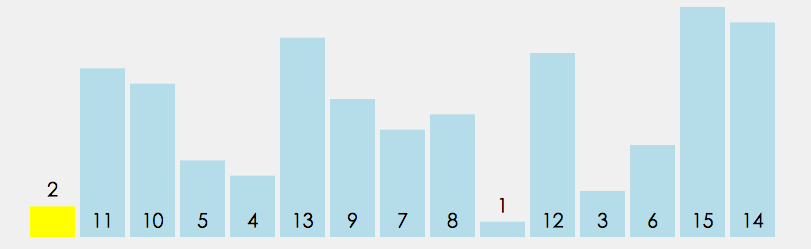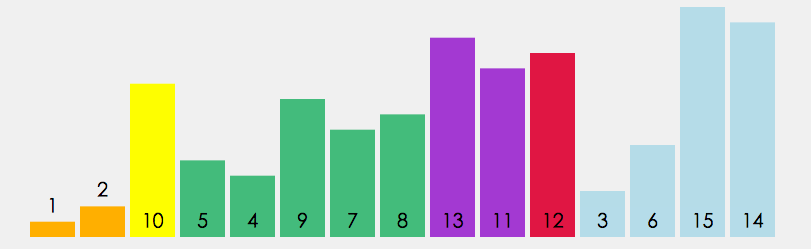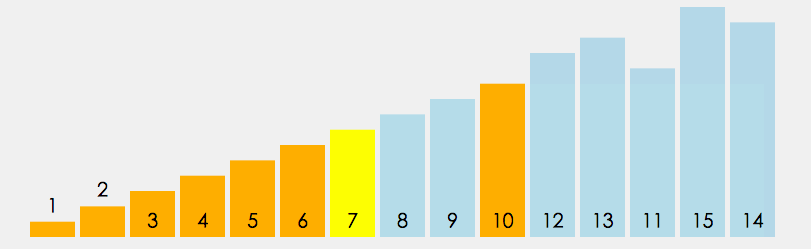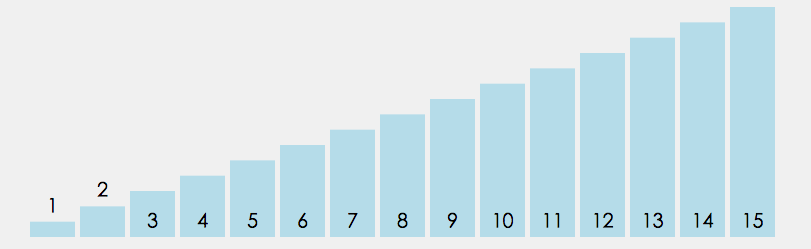
1 | /** 7、快速排序 **/ |

8、归并排序
归并排序建立在归并操作之上, 它采取分而治之的思想, 将数组拆分为两个子数组, 分别排序, 最后才将两个子数组合并; 拆分的两个子数组, 再继续递归拆分为更小的子数组, 进而分别排序, 直到数组长度为1, 直接返回该数组为止.
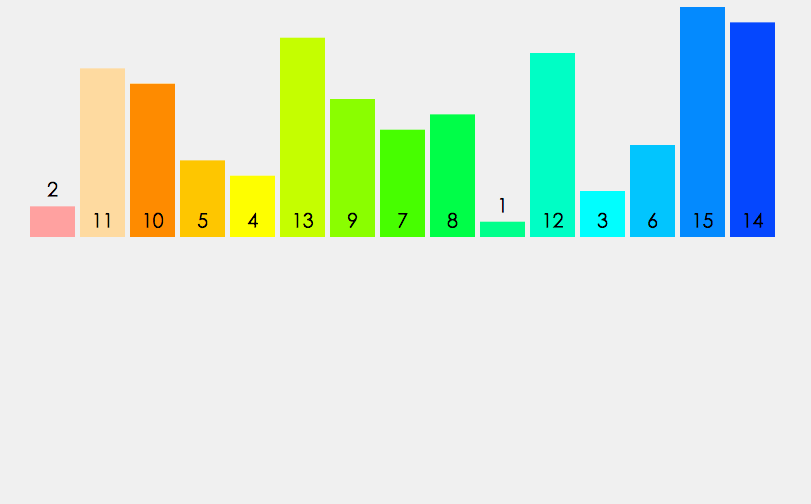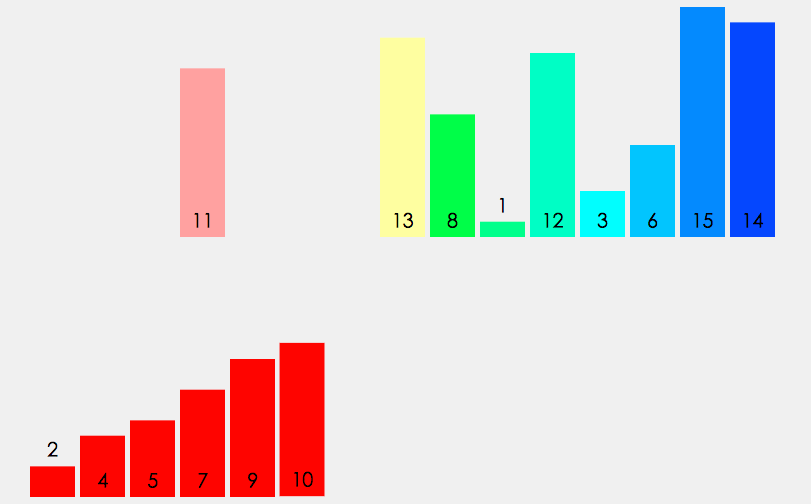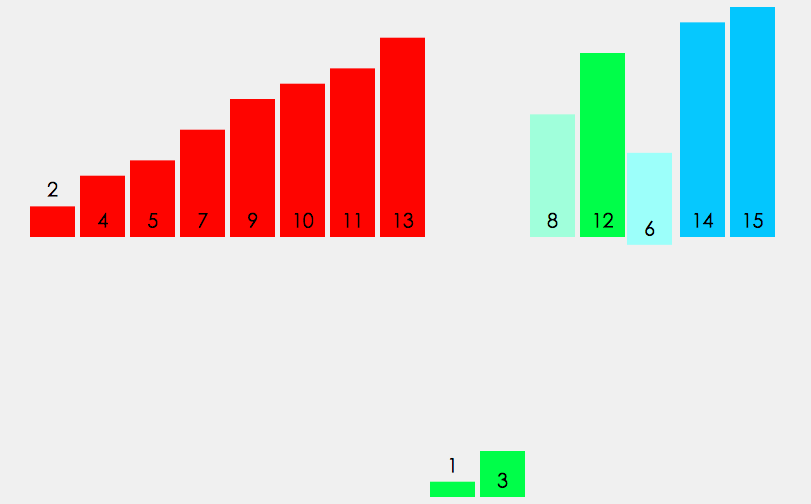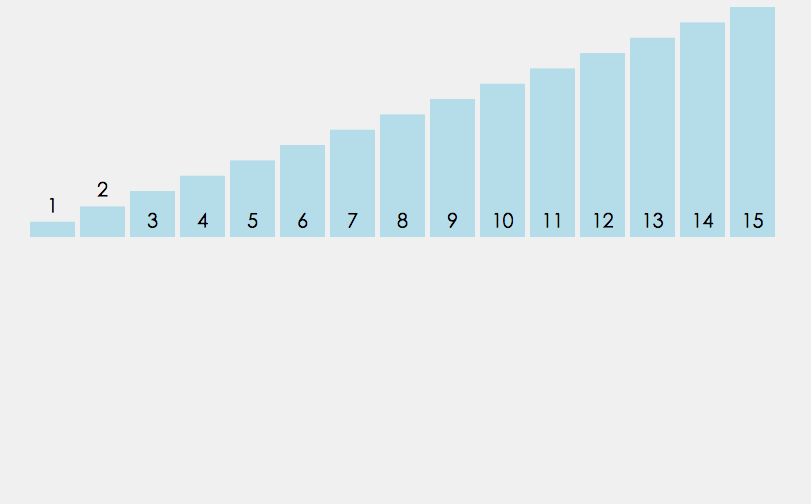
1 | /** 8、归并排序 **/ |

9、堆排序
10、计数排序
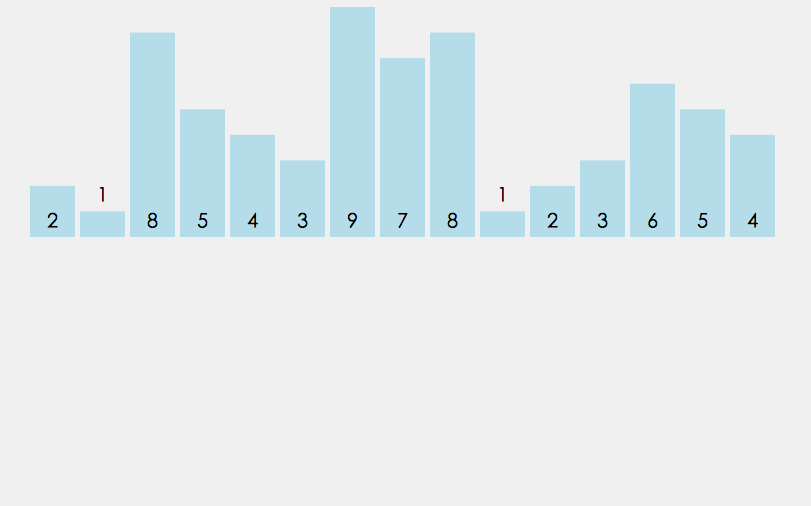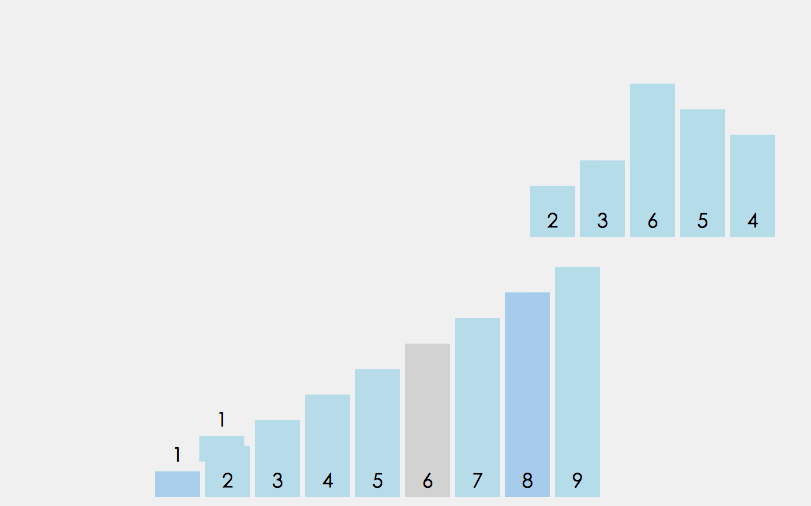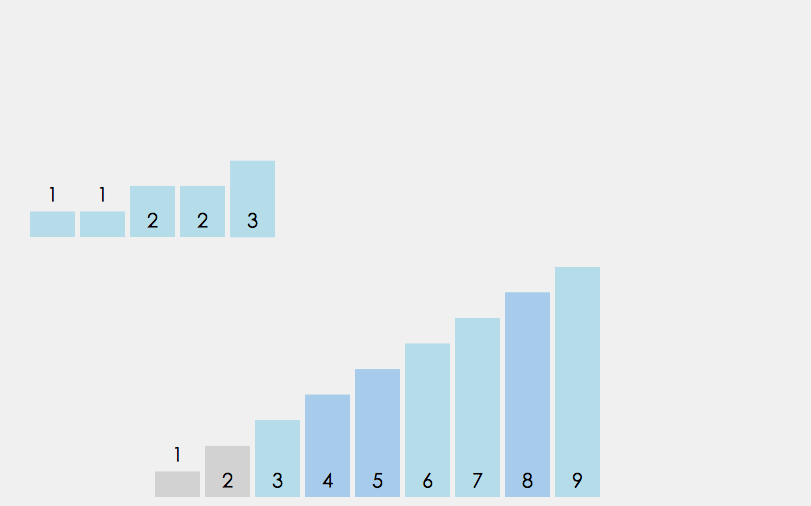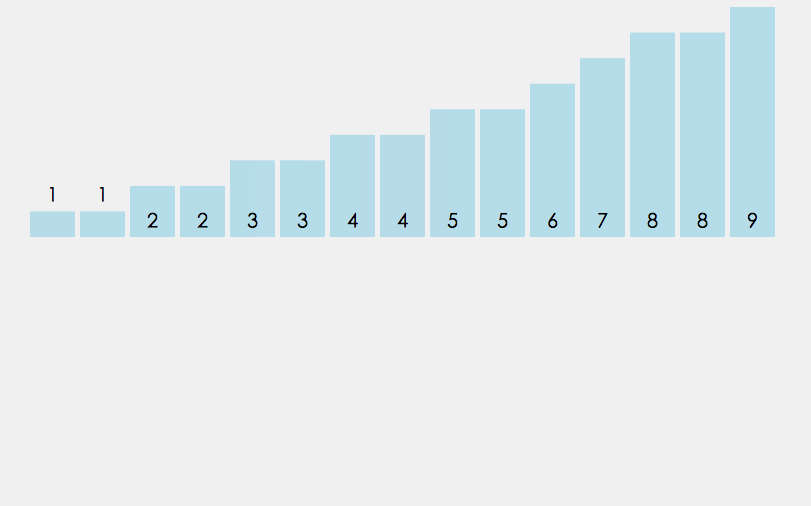
计数排序利用了一个特性, 对于数组的某个元素, 一旦知道了有多少个其它元素比它小(假设为m个), 那么就可以确定出该元素的正确位置(第m+1位)
- 获取待排序数组A的最大值, 最小值.
- 将最大值与最小值的差值+1作为长度新建计数数组B,并将相同元素的数量作为值存入计数数组.
- 对计数数组B累加计数, 存储不同值的初始下标.
- 从原数组A挨个取值, 赋值给一个新的数组C相应的下标, 最终返回数组C.
11、桶排序
桶排序即所谓的箱排序, 它是将数组分配到有限数量的桶子里. 每个桶里再各自排序(因此有可能使用别的排序算法或以递归方式继续桶排序). 当每个桶里的元素个数趋于一致时, 桶排序只需花费O(n)的时间. 桶排序通过空间换时间的方式提高了效率, 因此它需要额外的存储空间(即桶的空间).
12、基数排序
基数排序源于老式穿孔机, 排序器每次只能看到一个列. 它是基于元素值的每个位上的字符来排序的. 对于数字而言就是分别基于个位, 十位, 百位 或千位等等数字来排序. (不明白不要紧, 我也不懂, 请接着往下读)